The Ammeter in the Figure(Figure 1) Reads 4.0 a .
Concepts and reason
The concept used here is Kirchhoff's electric current law and Kirchhoff's voltage law. Firstly, employ Kirchhoff's current law to the left loop and Kirchhoff's voltage police to the correct loop and use the equation obtained from the loop to calculate the current \(I_{2}\). In the second role, calculate the value of \(\varepsilon\) by using the value of electric current calculated in the previous role.
Fundamentals
Kirchhoff'southward current law:
At whatsoever junction in circuit, the algebraic sum of currents will be zero. Kirchhoff'southward voltage police force:
In any closed loop of circuit, the algebraic sum of voltages volition be zero.
The following figure shows the given circuit diagram.
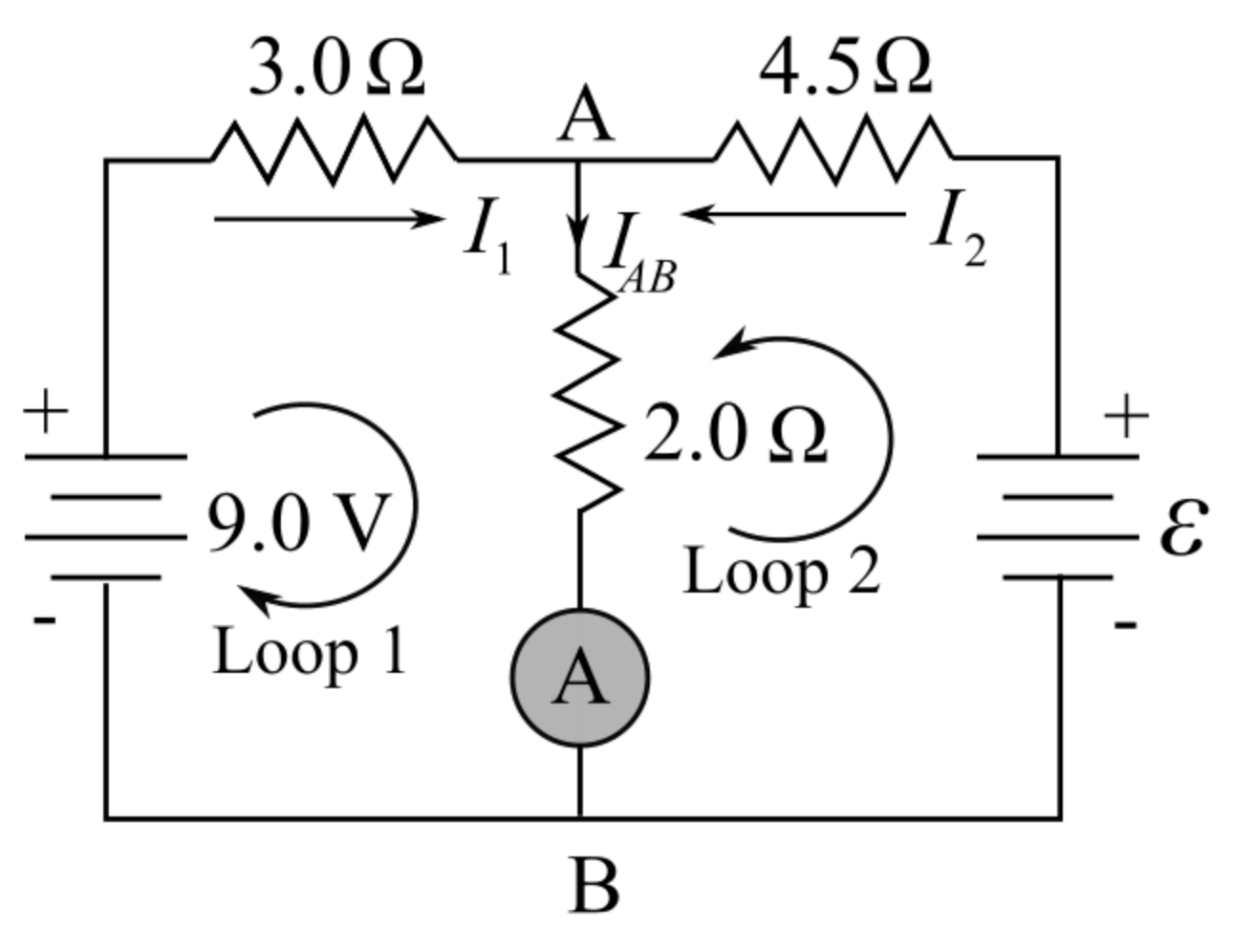
In this circuit diagram, signal A and B is shown, at point A both currents are coming and they will go through A to B.
a) The Kirchhoff'south electric current constabulary is used at junction \(\mathrm{A}\), it is written as, \(I_{1}+I_{2}=I_{A B} \ldots \ldots\) (i)
The current between \(\mathrm{A}\) and \(\mathrm{B}\), it ways the electric current \(I_{A B}\) volition be equal to the reading of attached ammeter, which is
\(3 \mathrm{~A}\). Therefore, information technology is written as, \(I_{A B}=3 \mathrm{~A}\)
The voltage difference between \(A\) and \(B\) is written as, \(V_{A B}=I_{A B} R_{A B}\)
Substitute \(3 \mathrm{~A}\) for \(I_{A B}\) and \(2 \Omega\) for \(R_{A B}\) in above expression.
$$ \begin{aligned} V_{A B} &=(3 \mathrm{~A})(2 \Omega) \\ &=half-dozen \mathrm{~5} \end{aligned} $$
Apply the Kirchhoff'due south voltage police in loop one , it is written as, \(ix \mathrm{~Five}-3 I_{1}=V_{A B}\)
Substitute the value \(6 \mathrm{~5}\) for \(V_{A B}\) in higher up expression.
$$ \begin{array}{c} 9 \mathrm{~V}-3 I_{1}=6 \mathrm{~V} \\ 3 I_{ane}=three \mathrm{~Five} \\ I_{i}=one \mathrm{~A} \end{array} $$
Substitute the value \(3 \mathrm{~A}\) for \(I_{A B}\) and \(one \mathrm{~A}\) for \(I_{1}\) in expression (1)
\(1 \mathrm{~A}+I_{2}=3 \mathrm{~A}\)
$$ I_{2}=2 \mathrm{~A} $$
Part a The value of \(I_{2}\) is \(2 \mathrm{~A}\).
Apply the Kirchhoff'due south current constabulary to find the relation betwixt currents, utilise the Kirchhoff's voltage law and calculate \(I_{ane}\) and with the assist of \(I_{ane}\), calculate the value \(I_{two}\).
(b) Apply the Kirchhoff's voltage law in loop 2 , it is written as, \(\varepsilon-four.5 I_{two}=V_{A B}\)
Substitute the value \(6 \mathrm{~V}\) for \(V_{A B}\) and \(2 \mathrm{~A}\) for \(I_{two}\) in above expression.
$$ \begin{array}{c} \varepsilon-4.5(2 \mathrm{~A})=vi \mathrm{~5} \\ \varepsilon=15 \mathrm{~V} \end{assortment} $$
Part b The value of \(\varepsilon\) is \(xv \mathrm{~V}\).
Apply the Kirchhoff's voltage law and calculate \(I_{ane}\) and with the help of \(I_{i}\), calculate the value \(I_{ii}\). Apply the Kirchhoff's voltage law in loop 2 and calculate the \(\varepsilon\).
Source: https://wizedu.com/questions/147/the-ammeter-in-the-figure-reads-30a
0 Response to "The Ammeter in the Figure(Figure 1) Reads 4.0 a ."
Enviar um comentário